此篇复习

随机变量X

射手打靶，服从分布： X~（5 7 9|0.2 0.6 0.2） 5 7 9就是随机变量的取值，后面是对应的概率。

概率密度函数（PDF）

概率密度通俗的说就是随机变量X恰好取得（X = A）某个值的概率的导数，不严格的说取微分就是概率。 设$F(x)$是随机变量X的累计分布函数（CDF），如果存在非负可积函数$f(x)$对任意实数x有： $F(x) = \int_{-\infty }^{x}f(t)dt$ 其中$f(x)$就是X的概率密度函数。 PDF图像中曲边梯形的面积就是X落在对应区间的概率。

累计分布函数（CDF）

累积分布函数是实数随机变量X的概率分布，是概率密度函数的积分。记$F(X)$，则： $F(x) = P(X \le x), -\infty< x <+\infty$ 这意味着CDF(x)代表着，采样落在X<=x的概率。

随机变量数字特征

数学期望

数学期望通俗的说就是平均数。 离散随机变量X数学期望如下算： $\bar{X} = \sum_{i = 1}^{r}x_{i}P(X = x_{i}) = \sum_{i = 1}^{r}x_{i}p_{i}$ 上述最后的数列求和若收敛则期望存在，否则不存在。

连续随机变量X的数学期望如下算： $E(X) = \int_{-\infty}^{+\infty}xf(x)dx$

对于随机函数（自变量为随机变量的函数）的数学期望，则有下列公式： 设离散随机变量$X$的分布律为$P(X=x_{k}) = p_{k},k = 1,2,…$，若$Y = g(X)$的数学期望$E[g(X)]$存在，则有： $E[g(X)] = \sum_{k}^{}g(x_{k})p_{k}$ 设连续随机变量$X$的概率密度为$f(x)$，$Y = g(X)$的数学期望$E[g(X)]$存在，则 $Y$的数学期望为： $E[g(X)] = \int_{-\infty}^{+\infty}g(x)f(x)dx$

后面的MC会用到上述定理。

方差

方差用来刻画变量偏离均值的程度。设$X$是一个随机变量，若$E[X-E(X)]^2$存在，则称其为$X$的方差，记为$D(X)$，即： $D(X) = E[X - E(X)]^2$ 方差开方成为标准差，一般记为$\sigma _{X}$.

若随机变量的分布为$P(X=x_{k}) = p_{k},k = 1,2,…$，则： $D(X) = \sum_{k}^{}[x_{k} - E(X)]^2p_{k}$ 若连续随机变量的PDF为$f(x)$，则： $D(X) = \int_{-\infty}^{+\infty}[x - E(X)]^2f(x)dx$

公式

$D(X) = E(X^2)-[E(X)]^2$ $E(aX) = aE(X),D(aX) = a^2D(X)$ 若随机变量X的方差$D(X)=0$的充要条件是存在常数C，使得 $P(X=C)=1$

大数定理和中心极限定理

切比雪夫不等式

翻书。

大数定理

翻书。

中心极限定理

中心极限定理表明，当n充分大的时候，$Y_{n}$近似服从标准正态分布。这解释了客观世界中为什么许多随机变量都服从或者近似服从正态分布。

二维随机变量和随机变量独立性及其应用

二维随机变量

设$F(x,y)$是二维随机变量$(X,Y)$的分布函数，如果存在非负函数$f(x,y)$，使： $F(x,y) = \int_{-\infty}^{x}\int_{-\infty}^{y}f(u,v)dudv$ 则称(X,Y)为二维连续型随机变量，f(x,y)为(X,Y)的联合概率密度（联合PDF）。 $X$的边缘概率密度 $f_{X}(x)=\int_{-\infty}^{+\infty}f(x,y)dy$ $Y$的边缘概率密度 $f_{Y}(y)=\int_{-\infty}^{+\infty}f(x,y)dx$

边缘概率密度代表了对于指定的一个随机变量，其他随机变量覆盖所有可能的情况的平均概率密度。

随机变量的独立性

设$F(x,y)$及$F_{x}(x),F_{y}(y)$分别是二维随机变量$(X,Y)$的$CDF$和边缘$CDF$，若对任意的$x,y$有 $P(X \le x,Y \le y) = P(X \le x)P(Y \le y)$ 即 $F(x,y) = F_{X}(x)F_{Y}(y)$ 则称随机变量$X$和$Y$是相互独立的。 也就是说，在对一个取值的时候对第二个完全没有影响。 若$f(x,y)及f_{X}(x),f_{Y}(y)$分别是$(X,Y)$的概率密度及边缘概率密度，$X$和$Y$相互独立的充要条件为 $f(x,y) = f_{X}(x)f_{Y}(y)$

条件概率

$p(y|x)=\frac{p(x,y)}{p(x)}$

采样联合分布函数，一般就是先求一个边缘概率密度，使用1D方法进行采样；使用条件概率公式求出另外一个分布，同样做1D采样。

统计估值

从总体X中随机抽取n个个体$X_{i}$，$i = 1,2,…,n$，这个n个个体就称为总体X的一个容量为n的样本，此过程称为抽样。这里的每一个$X_{i}$都是随机变量，因为第i个被抽到的个体$X_{i}$的取值事先是无法预知的。对样本$X_{i}$，$i = 1,2,…,n$进行一次观测得到的确切数值记录为:$x_{i}$，$i = 1,2,…,n$，称为样本观值测。当$X_{i}$，$i = 1,2,…,n$相互独立且与总体同一分布的时候，这组样本称为简单随机样本。这个过程就称为简单随机抽样。

设$X_{i}$，$i = 1,2,…,n$来自总体X的样本，$x_{i}$，$i = 1,2,…,n$是观测值，已知函数$g(t_{1},t_2,…,t_n)$是已知n元函数，称$g(X_1,X_2,…,X_n)$是样本函数，$g(x_1,x_2,…x_n)$是样本观测函数。若样本函数中不含有未知参数，则称为统计量。（常用的统计量包括期望方差等在教科书可以查到。）

说了统计量下面来说很重要的概念——估计量（estimator）。 统计推断中包括参数估计和假设检验。参数估计：通过构造统计量来估计总体未知参数的值或者范围。

• 值：点估计
• 范围：区间估计

区间估计不说，只说点估计。 设X为总体，$\theta$是总体分布中所含的未知参数（可向量）。$X_{i}$，$i = 1,2,…,n$是取自总体X的一个样本，$x_{i}$，$i = 1,2,…,n$是相应的观察值。为了通过观察值$X_{i}$，$i = 1,2,…,n$估计出位置参数$\theta$，先构造一个合适的统计量： $\hat{\theta}=\hat{\theta}(X_1,X_2,...,X_n)$ 然后使用其观测值$\hat{\theta}=\hat{\theta}(x_1,x_2,...,x_n)$来估计$\theta$的值。 $\hat{\theta}=\hat{\theta}(X_1,X_2,…,X_n)$就是参数$\theta$的估计量。 $\hat{\theta}=\hat{\theta}(x_1,x_2,…,x_n)$就是参数$\theta$的估计值。 估计方法很多，但是这里并不是很关注，所以不写。 在蒙特卡洛方法讲述蒙特卡洛方法的时候，提到了Horvitz-Thompson estimator就是一种估计量。

Horvitz-Thompson估计量 参考： https://en.wikipedia.org/wiki/Horvitz%E2%80%93Thompson_estimator

点估计中，同一参数不同方法可能得到不同估计量，因此要选出最优的。有三个基本的标准：

无偏性

由于估计量的取值由随机变量样本决定，所以具有随机性，所以希望估计值在平均意义下等于其真值，即$E(\hat{\theta})=\theta$.如此$\hat{\theta}$称为$\theta$的无偏估计量。

有效性

$\hat{\theta_1}=\hat{\theta_1}(X_1,X_2,…,X_n)$和$\hat{\theta_2}=\hat{\theta_2}(X_1,X_2,…,X_n)$都是未知参数$\theta$的无偏估计量，若$D(\hat{\theta_1}) < D(\hat{\theta_2}) $，则$\hat{\theta_1}$比$\hat{\theta_2}$有效。

一致性

注意估计量还依赖于样本容量，人们希望n充分大的时候，估计值与真实值充分接近，这叫做一致性。 设$\hat{\theta_n},n=1,2,…$是未知参数$\theta$的一列估计量，若$\hat{\theta_n}$依概率收敛于$\theta$，即： $\lim_{n \to \infty }P(|\hat{\theta_n}-\theta|<\varepsilon )=1$ $\hat{\theta_n}$是未知参数$\theta$的一致估计量。

采样方法

采样的根本目的就是————生成一个服从指定的分布$F(x)$的随机数。

均匀采样

蒙特卡洛方法理论和应用，康崇禄，科学出版社，2015.01 第二章 随机数生成和检验

均匀分布是其他的随机生成的基础，但其本身是一个世界难题，一般方法生成的随机数都是伪随机数，但是实际效果不错。

srand(time(NULL);
double randuni()
{
    return rand()*1.0/(RAND_MAX*1.0);
}
//更加精确的方案
RandNum rng;
double randuni()
{
    return 1.0*rng.randLong(0x7fffffff)/(1.0*0x7fffffff);
}

每一个数的概率都是一样的，这些数是均匀分布在0，1区间的,前者的间隔为1/RAND_MAX,后者的间隔为1/0x7fffffff;这里注意等间隔的条件也是很重要的，因为：例如1/rand()(或1/rng.randLong(0x7fffffff))产生的是（0，1）之间的数，且每一个数的概率相同，但是，很显然的是它并不是均匀的散布在（0，1）之间的，所以他也不能说是U（0，1）分布。 注意事项：如果标准库有提供那么请使用标准库提供的函数…

逆分布法

逆分布如下：

1. 产生服从U(0,1)分布的随机变量u
2. 累计分布函数$F(X)$的逆分布为$iF(u)$，计算$X = iF(u)$

那么结果X就是服从累计分布函数$F(X)$的随机数. 不是很严格的证明如下：如果从均匀分布中采样一个数想要和在分布p（PDF）下采样一个数等价，那么我们只需要两者的概率相等就可以，即：$p(y)dy=u(x)dx\rightarrow p(y)=u(x)\frac{dx}{dy}$ 我们想要求一个$y=f^{-1}(x)$,于是有$x=f(y)\rightarrow \frac{dx}{dy}=f’(y)$,于是：$p(y)=u(x)f’(y)$,移项后两端对y做$-\infty$到$y$的积分有：$\int_{-\infty}^y \frac{p(y)}{u(x)}dy = \int_{-\infty}^y f’(y)dy$.注意到右边得到分布原函数$f(y)=Pr(Y<=y)$，左边$u(x)=1$(pdf已经归一化):$f(y)=P(y)$,所以，$y=P^{-1}(x)$.

一般的转换参考：http://claireswallet.farbox.com/post/math/an-fen-bu-cai-yang#toc_1

接受/拒绝法

对于一些函数，比如正态分布，我们无法求出他的反函数，他连初等形式都没有。于是我们可以使用拒绝法进行采样生成随机数。 设$f(x)$为需要生成的随机数的密度函数（PDF），这里就对应上面的积分中的部分，又设另外一个容易采样的随机变量的函数为建议分布$g(x)$，且存在常数c使得$f_{X}(x)\le cg_{Y}(x)$成立的话，那么有如下算法：

1. 从g中产生随机数
2. 产生均匀分布随机数$u～U(0,1)$
3. 若$u·cg_{Y}(y)<f_{X}(y)$(这时他落到下图非灰色区域，这时的)，则$X=y$；否则重返步骤1.

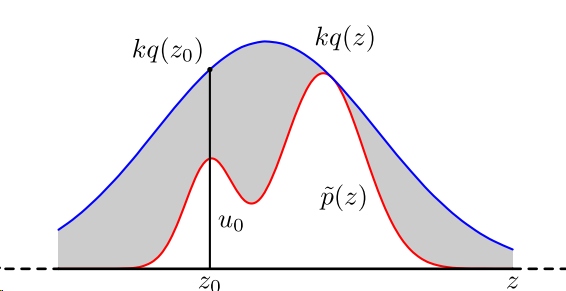
证明： 上述过程以概率P(X<x)产生了一个随机数，这个过程中返回的值要求满足$u<\frac{f_{X}(y)}{cg_{Y}(y)}$才给予返回，所以是在$u<\frac{f_{X}(y)}{cg_{Y}(y)}$条件下的$y<x$条件概率。而1.2步骤产生的随机数都是相互独立的，所以有联合概率密度$I(0<u<1)g_{Y}(y)$. 所以最后有： $P(X<x)=P(y<x|u<\frac {f_{X}(y)}{cg_{Y}(y)}) = \frac{P(y<x,u\le \frac{f_{X}(y)}{cg_{Y}(y)})}{P(u\le \frac{f_{X}(y)}{cg_{Y}(y)})}$ 把上述式子展开，得到如下结果：

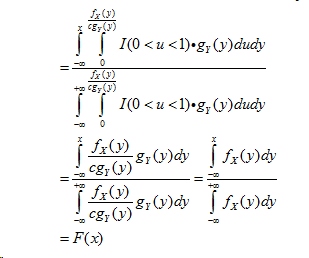可以看到上面的$F(x)$的确是一个CDF。

这种方法，在高纬情形下，一般难以找到一个好的建议分布，c值也不好合理确定，所以可能会导致拒绝率很高。

俄罗斯赌轮选择法

和赌轮一样，轮盘上面积越大的区域小球停在其中的概率就越大。

--赌轮选择
function Test1:select()
    local piece = math.random()*self.total_fitness
    local temp = 0
    
    for i=1,#self.genomes do
        temp = temp + self.genomes[i].fitness
        
        if temp>=piece then
            return self.genomes[i]
        end
    end
end

重要性采样

借助一个容易抽样的分布q（pdf）。得到一个公式： $E(f) = \int f(z)p(z)dz=\int f(z)\frac{p(z)}{q(z)}dz=\frac{1}{L}\sum_{l=1}^{L}\frac{p(z^l)}{q(z^l)}f(z^l)$ 其中$\frac{p(z)}{q(z)}$可以看做important weight。p 和 f 是确定的，我们要确定的是 q.

更多见：http://claireswallet.farbox.com/post/math/meng-te-qia-luo-fang-fa

蒙特卡洛积分估计

设有积分： $I=\int_{\Omega}f(x)d\mu(x)$

被积函数$f(x)$在s维立体空间$\Omega$上定义，那么上述函数即为多维积分。 把多维积分写为： $I=\int_{\Omega}h(x)p(x)d\mu(x)$

现在要使用随机采样的方法来计算这个积分。

在$p(x)$分布下抽样随机变量X，只要$p(x)$比较容易采样即可。

从概率密度函数$p(x)$抽样产生随机变量样本值$x_i$，计算$h(x_i)$，采样n次，使用下列估计量来估计分布期望： $\hat {I} = (1/n)\sum_{i=1}^{n}h(X_i)$

平均值方法最主要的工作是确定概率密度函数$p(x)$和$h(x)$。 这里$h(x)=\frac{f(x)}{p(x)}$

注意： $E[\hat{I}]=E[\frac{1}{n}\sum_{i=1}^n\frac{f(x)}{p(x)}]=\frac{1}{n}\sum_{i=1}^nE[\frac{f(x)}{p(x)}]$ 现在使用Law of the unconscious statistician将$E[\frac{f(x)}{p(x)}]$展开得到$\frac{1}{n}\sum_{i=1}^n\int_{\Omega}\frac{f(x)}{p(x)}p(x)dx=I$. 依据强大数定理，此估计量以概率1收敛与期望。

于是： $\hat {I} = (1/n)\sum_{i=1}^{n}\frac{f(x)}{p(x)})$

[1]中提到（参考文献也在里面P37底部），这种估计量在调查抽样文献中第一次出现被称作 Horvitz-Thompson估计量 参考： https://en.wikipedia.org/wiki/Horvitz%E2%80%93Thompson_estimator 更多的资料可以参考[6]的Chapter11.

采样N次，那么对应的估计量就是：

注意这里使用$F_N$强调其是一个随机变量，他的值根据采样情况变化。这个估计量得到的所有随机变量观测值可以推测一个估计值出来，这个估计值就是统计意义上的近似积分值。

这个方法叫做“平均值法”，有别于另一种“投针法”.

为了使得估计量最优的，需要满足一些标准(参考：概率论与数理统计基础摘要，[1]2.4)：

无偏性

这个很容易给出。 下面给出估计项的期望： $E[F_{N}] = E[\frac{1}{N}\sum_{i=1}^{N}\frac{f(X_{i})}{p(X_{i})}]$ $=\frac{1}{N}\sum_{i=1}^{N}\int_{\Omega}\frac{f(x)}{p(x)}p(x)d\mu(x)$ $=\int_{\Omega}f(x)d\mu(x) = I$ $where f(x) != 0$

一致性

$Pr (\lim_{n \to \infty }F_N =I)=1$ 他的充分条件是： $\lim_{n \to \infty }\beta[F_N]=\lim_{n \to \infty }V[F_N]=0$

有效性

有效性就是尽量减小方差。这个在后面会主要说。

权衡效率

蒙特卡洛积分的效率权衡可以用下列量： $\varepsilon[F] = \frac{1}{V[F]T[F]}$ $T[F]$是计算F需要的时间。

优缺点

优点：

• 任何维度复杂度都是$O(N^{-1/2})$；支持间断函数。 收敛性将在之后讨论。
• 积分简单，只需要两个操作——采样和点估计。This encourages the use of object-oriented black box interfaces。
• 具有一般性。受几何条件限制小。
• 误差容易确定。
• 易于实现。 缺点：
• 收敛速度慢
• 误差具有概率性

收敛速度

参考[1]2.4.1

有效性（减小方差）

设计一个高效的估计量是蒙特卡洛方法研究的基本目标。这些技术一般被称作方差消减技术（variance reduction methods）。这里讲述的所有技术都是用到图形学中的技术。 这些方法可以按照4种主要思想分为几类：

• analytically integrating a function that is similar to the integrand;（分析性地积分一个类似被积函数的函数）【including the use of expected values, importance sampling, and control variates】
• uniformly placing sample points across the integration domain;
• adaptively controlling the sample density based on information gathered during sampling; and
• combining samples from two or more estimators whose values are correlated.

多数方差消减技术都是最早用到survey sampling文献中的，这些东西早在蒙特卡洛方法出现之前就有了。例如分层采样stratified sampling ,importance sampling,control variates等。

其他

蒙特卡洛方法需要计算下列3个步骤：

• 根据概率分布采样
• 在采样点处计算函数值
• 平均这些有合适加权的采样值

采样

下面来看消减方差的技巧。

提升蒙特卡洛方法的效能

参考资料

[1] ROBUST MONTE CARLO METHODS FOR LIGHT TRANSPORT SIMULATION

[2] Monte Carlo Methods in Rendering

[3] Introduction to Monte Carlo methods

[4] PBRT

[5] 蒙特卡洛方法理论和应用，康崇禄，科学出版社，2015.01

[6] William G. Cochran (1977), Sampling Techniques, 3rd Edition, Wiley. ISBN 0-471-16240-X