现在的水平还不可能深入理解积分方程论，而是为了确保在将来遇到的时候知道这个东西到底是什么，应该使用什么方法来解决，同时也可以加深对问题的理解。

积分变换

算子

设$U,V$是两个线性空间。任何从$U$到$V$的映射都叫做算子（operator）。 下列例子都是算子：

• 期望，方差，协方差，标准差，阶乘
• $\frac{d}{dt^{‘}}$以及$\int_{0}^{t}$
• 傅里叶变换和拉普拉斯变换
• 梯度，旋度，散度
• 一种积分变换

积分变换

下列形式： $(Tf)(u)=\int_{t1}^{t2}K(t,u)f(t)dt$ 称为积分变换。 其中$f$是输入函数，$Tf$是输出函数。一个积分变换是一种特殊的算子。 通过制定不同的$K(t,u)$(两个变量)我们可以得到各种有用的积分变换，这个东西就是kernel。也叫做kernel function, integral kernel or nucleus of the transform.。 某些变换有逆变换： $f(t)=\int_{u1}^{u2}K^{-1}(u,t)(Tf)(u)du$ 如果ut交换仍然相等，这种kernel我们叫做 symmetric kernel . 如果交换后，要加个负号才相等则叫做埃米尔特的。

有了积分变换，我们就可以很方便地描述一些复杂的问题。

下面有个表有各种积分变换，对应指出了他们各自的核以及逆核：

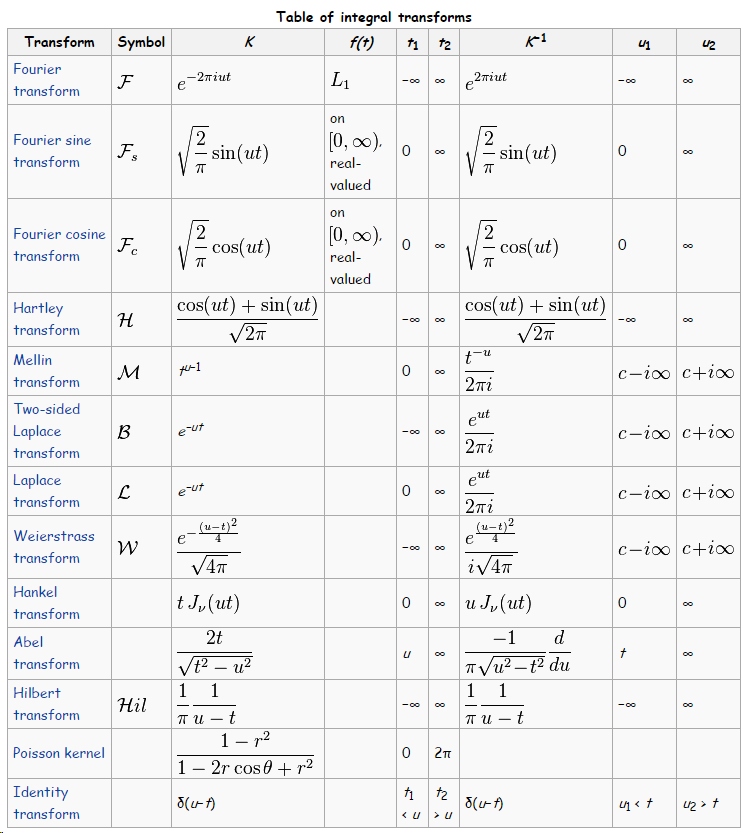
很明显，卷积也是一种积分变换，他的变换kernel是形式如$h(x-t)$的函数.

积分方程

积分方程是指未知函数出现在积分好下的方程。有时候同一个问题既可以表示成积分方程也可以表示成微分方程，但并非总能这么做。 下面我们用$\phi$表示未知函数，用$f$表示已知函数。 $\lambda \int_{a}^{b}K(x,t)\phi(t)dy+f(x)=0$ 这种未知函数仅出现在积分号内的，称为第一类积分方程。 $\phi(x) = \lambda \int_{a}^{b}K(x,t)\phi(t)dt+f(x)$ 这种未知函数即出现积分内又在外的，称为第二类积分方程。如果上式去掉f，则叫做齐次第二类方程。 其中$K(x,t)$称为kernel。置于为什么称为kernel有前面的积分变换普遍应该很清楚了。

如果积分限$a/b$都是常数称为Fredholm方程，积分限有一个是变量的，叫做Volterra方程。 如果$a \le x \le t \le b$时，$k(x,t)$等价于0，则Volterra退化为Fredholm。因此，前者可以看成后者的特殊情形，但是前者有独特之处，所以分开讨论的。 对于Fredholm方程，第二类方程理论比较完整玩呗，而第一类则不够。但是很多数学物理反问题都需要第一类方程。对于Voloterra方程，第一类则多可以转化为第二类。

积分方程还可以按照kernel的性质来分类： 但那个是$(x,t)$的连续函数时，或者在区域xt在ab的闭区间中虽不连续但是平方可积，即： $\int_{a}^{b} \int_{a}^{b} |k(x,t)|dxdt$ 存在且有限时，kernel为非奇异kernel或者Fredholm kernel。 若是如下形式： $k(x,t)=\frac{h(x,t)}{|x-t|^a}$ 其中$h(x,t)$有界，常数在(0,1)，则叫称为弱奇性kernel。 当具有如下形式： $k(x,t)=\frac{a(x,t)}{x-t}$ 其中$a(x,t)$关于xt的偏导数存在： $\int_a^b k(x,t) \phi(t)dt = \int_a^b \frac{a(x,t)}{x-t}\phi(t)dt$ 在通常意义下是发散的，如果对$\phi(x)$加上一定限制，可以使得 $\lim_{\varepsilon \to 0}[\int_{a}^{x-\varepsilon} k(x,t)\phi (t)dt + \int_{x+\varepsilon}^bk(x,t)\phi(t)dt]$ 存在，此时$k(x,t)$称为Cauchy奇性kernel。 这三种kernel就对应了三种方程。

积分方程来源的最简单例子就是贮存问题： 一个商店销售商品，设进货与销售是一个连续过程，买进的商品可以立即销售。设商店购进商品后，在t时刻尚未出售的商品比例为$k(t)$。现在要求确定商品进货的速率$\phi(t)$，使得商店存的商品总价值不变。 设商店t=0时开始营业，在时间间隔$[\tau,\tau + d\tau]$内，商店购进商品的价值为$\phi(\tau)d\tau$这些商品因为出售而减少。在时刻$t > \tau$时，未售出的商品价值为： $k(t-\tau)\phi(\tau)d\tau$ 因此，在时刻t未售出的商品和购进商品的价值之和： $Ak(t)+\int_0^t k(t-\tau)\phi(\tau)d\tau$ 如果任何时刻，总价值不变，就应该满足下列方程： $A = Ak(t)+\int_0^t k(t-\tau)\phi(\tau)d\tau$ 这显然是一个第一类Volterra积分方程。

下面看一些比较熟悉的方程，更多关于积分方程的内容参考【1】。

卷积

$y(t)=\int_{-\infty}^{\infty}x(p)h(t-p)dp=x(t)*h(t)$ 可以发现，这是一个积分变换。h(t-p)是它的kernel。

渲染方程

渲染方程 $L_o(x,\omega_o,\lambda,t)=L_e(x,\omega_o,\lambda,t)+\int_{\Omega}f_r(x,\omega_i,\omega_o,\lambda,t)L_i(x,\omega_i,\lambda,t)(\omega_i·n)d\omega_i$

• $\lambda$是波长
• $t$是时间
• $x$是空间位置
• $n$是表面法线
• $\omega_o$出射方向
• $\omega_i$入射反方向
• $L_o(x,\omega_o,\lambda,t)$出射光谱辐射度，波长为$\lambda$
• $L_e(x,\omega_o,\lambda,t)$发射光谱辐射度。

是第二类Fredholm方程。 有两种数值方法可以解，有限元和随机walk through。 前者主要是辐射度算法，后者主要是蒙特卡洛方法，具体的包括有路径跟踪，光子图，Metropolis光线传输算法等等。

Refrence

【1】沈以淡.积分方程（第二版）.北京理工大学出版社.2002.6.