矩阵及变换，以及矩阵在DirectX和OpenGL中的运用

1。矩阵和线性变换：一一对应

矩阵是用来表示线性变换的一种工具，它和线性变换之间是一一对应的。 考虑线性变换： a11x1 + a12x2 + …+a1nxn = x1’ a21x1 + a22x2 + …+a2nxn = x2’ … am1x1 + am2x2 + …+amn*xn = xm’

对应地，用矩阵来表示就是：

a11 a12 … a1n		x1		x1’
a21 a22 … a2n		x2		x2’
…	*	…	=	…
am1 am2 … amn		xn		xm’

也可以如下来表示：

               |a11 a21 ... am1|
               |a12 a22 ... am2| |x1 x2...xn|*|...                   |= |x1' x2'... xm'|
               |a1n a2n ... amn|

其中涉及到6个矩阵。分别为A[mn],X[n1],X’[m1]以及X[1n],A[nm],X’[1m]。 可以理解成向量x(x1,x2,…,xn)经过一个变换矩阵A[mn]或A[nm]后变成另外一个向量x’(x1’,x2’,…,xm’))。

2。矩阵的表示法：行矩阵 vs. 列矩阵

行矩阵和列矩阵的叫法是衍生自行向量和列向量。 其实，矩阵A[mn]可以看成是m个n维的row vector构成的row matrix，也可看成是n个m维的column vector构成的column matrix。 其中，X[n1]/X’[m1]就等价于1个n/m维的column vector。X[1n]/X’[1*m]就等价于1个n/m维的row vector。 Row matrix和Column matrix只是两种不同的表示法，前者表示把一个向量映射到矩阵的一行，后者表示把一个向量映射到矩阵的一列。 本质上体现的是同一线性变换。矩阵运算规定了它们可以通过转置运算来改变这个映射关系。

3。矩阵的相乘顺序：前乘或左乘 vs. 后乘或右乘

需要注意的是两种不同的表示法对应不同的运算顺序： 如果对一个column vector做变换，则变换矩阵(row matrix/vectors)必须出现在乘号的左边，即pre-multiply，又叫前乘或左乘。 如果对一个row vector做变换，则变换矩阵(column matrix/vectors)必须出现在乘号的右边，即post-multiply，又叫后乘或右乘。 一般不会弄错，因为矩阵乘法性质决定了相同的内维数的矩阵才能相乘。至于为什么是这个规律，为什么要row vector乘以column vector或column vector乘以row vector???想想吧。。。

所以左乘还是右乘，跟被变换的vector的表示形式相关，而非存储顺序决定。

4。矩阵的存储顺序：按行优先存储 vs. 按列优先存储

涉及到在计算机中使用矩阵时，首先会碰到存储矩阵的问题。 因为计算机存储空间是先后有序的，如何存储A[mn]的mn个元素是个问题，一般有两种：按行优先存储和按列优先存储。

row-major：存成a11,a12,…,amn的顺序。 column-major：存成a11,a21,…,amn的顺序。

这样问题就来了，给你一个存储好的矩阵元素集合，你不知道如何读取元素组成一个矩阵，比如你不知道a12该放在几行几列上。 所以，每个系统都有自己的规定，比如以什么规则存储的就以什么规则读取。DX使用Row-major,OGL使用Column-major.即一个相同的矩阵A[m*n]在DX和OGL中的存储序列是不一样的,这带来了系统间转换的麻烦。

不过,一个巧合的事情是:DX中，点/向量是用Row Vector来表示的，所以对应的变换矩阵是Column Matrix/Vectors,而OGL中，点/向量是用Column Vector来表示的，所以对应的变换矩阵是Row Matrix/Vectors.所以,如果在DX中对一个向量x(x1,x2,x3,1)或点(x(x1,x2,x3,1))应用A[44]的矩阵变 换，就是x’ = x(x1,x2,x3,1) * A[44],由于采用Row-major，所以它的存储序列是a11,a12,…,a43,a44。在OGL中，做同样的向量或点的变换，因为其使 用Row Matrix/Vectors,其应用的变换矩阵应该是A’[44] ＝ A[44]( ‘ 表示Transpose/转置)，就是x’ = A’[4*4] * x’(x1,x2,x3,1),但是由于采用Column-major,它的存储序列正好也是a11,a12,…,a43,a44!!! 所以实际上,对DX和OGL来讲,同一个变换,存储的矩阵元素序列是一样的.比如:都是第13,14,15个元素存储了平移变化量deltaZ,deltaY,deltaZ.

空间向量绕另一向量旋转

假定向量$P$绕单位向量$A$旋转角度$θ$，得到新的向量$P’$，则：

其中$A$为单位向量，旋转角度$θ$为逆时针方向旋转的角度。

假定向量$P$的坐标为$(px，py，pz)$，向量A的坐标为$(ax，by，cz)$

且：

则：

UE4实现代码：

inline FVector FVector::RotateAngleAxis( const float AngleDeg, const FVector& Axis ) const
{
    const float S    = FMath::Sin(AngleDeg * PI / 180.f);
    const float C    = FMath::Cos(AngleDeg * PI / 180.f);

    const float XX    = Axis.X * Axis.X;
    const float YY    = Axis.Y * Axis.Y;
    const float ZZ    = Axis.Z * Axis.Z;

    const float XY    = Axis.X * Axis.Y;
    const float YZ    = Axis.Y * Axis.Z;
    const float ZX    = Axis.Z * Axis.X;

    const float XS    = Axis.X * S;
    const float YS    = Axis.Y * S;
    const float ZS    = Axis.Z * S;

    const float OMC    = 1.f - C;

    return FVector(
        (OMC * XX + C ) * X + (OMC * XY - ZS) * Y + (OMC * ZX + YS) * Z,
        (OMC * XY + ZS) * X + (OMC * YY + C ) * Y + (OMC * YZ - XS) * Z,
        (OMC * ZX - YS) * X + (OMC * YZ + XS) * Y + (OMC * ZZ + C ) * Z
        );
}

Refs:

http://mathworld.wolfram.com/Matrix.html http://www.gamedev.net/community/forums/topic.asp?topic_id=321862

注意事项

• handness的判断，四指从x卷向y：
  • 如果用左手大拇指指向z，那就是左手系；
  • 如果用右手大拇指指向z，那就是右手系。

• AXB叉乘永远都只能使用下列公式：

  这个公式是坐标系无关的！也就是说，叉乘只能从u到v使用右手定则，AXB交叉为锐角。 也就是说——对于一个坐标系$(O,X,Y,Z)$:

  • 如果$X×Y=Z$，那么这个系就是右手系
  • 如果$X×Y=-Z$，那么这个系就是左手系

  所以，在计算叉乘的时候，要注意结果在数值上的方向。 方向，在左手系使用左手右手系使用右手，四指由A指向B，拇指即方向。 如果$A = (x,y,z),B=(x_1,y_1,z_1)$，那么在左手系中的叉乘就是： $(A×B)_{left-handed} = (zy_1-z_1y,z_1x-x_1z,x_1y-y_1x)$ $=(|\frac{y_1 z_1}{yz}|,|\frac{z_1x_1}{zx}|,|\frac{x_1y_1}{xy}|)$ 右手系，最直接可以记成下面这样： 左手系和右手系是相反的： $(u×v)_l = (v×u)_r$

• obj按照face来读取，一个立方体读取36个顶点而不是八个，因为他们的索引都不一样.
• 空间中有平面$Ax+By+C+D=0 $，点$P(x,y,z)$关于其对称点$P’(x_{1},y_{1},z_{1})$. $x_{1} = \frac{(B^2+C^2)x-A(Ax+By+Cz+D)}{A^2+B^2+C^2}$ $y_{1} = \frac{(A^2+C^2)y-B(Ax+By+Cz+D)}{A^2+B^2+C^2}$ $z_{1} = \frac{(B^2+C^2)z-C(Ax+By+Cz+D)}{A^2+B^2+C^2}$ 矩阵(左乘)如下：

• 投影w到v上公式：$v_{proj} = dot(v_{normal},w)v_{normal}$
• 线线距：叉乘找到公垂线，然后在线上各找一点组成向量往上面投影。

• 关于三角形 在一条线段上的点可以使用下列参数方程来表示： $Q=(1-t)A+tB,where 0\le t \le1$ 考察两条线段，AB和AC，有如下点集： $R = (1-s)(1-t)A + (1-s)tB+sC$ 这些点都在三角形ABC上，这就是三角形的参数方程。 算一下可以发现，这些ABC前面的系数，加起来是等于1的。 所以我们可以把这些点表示成下面这样： $P = \alpha A + \beta B + \gamma C,where \alpha/\beta/\gamma \ge 0$ 当$\alpha=0$时，点在BC上，以此类推。 这个时候$\alpha\beta\gamma $称为三角形ABC的重心坐标。

  

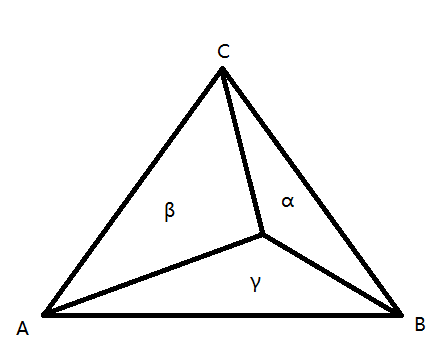
  还有一个规律是： 上面的$\alpha\beta\gamma $是面积对应的就是重心坐标。

• 齐次坐标是使用一个更高的维度来方便地表示底一维度中无穷远的一些问题。在齐次坐标$(x,y,z,w)$中：
  • 如果w=0，代表一个向量，两个点相减，w成0，则结果就是一个向量；乘以一个平移矩阵，结果不变，因为向量的平移本身就是没什么意义的。
  • 否则w=1，代表一个点，一个点加一个向量，是0+1=1，则结果还是点；乘以一个矩阵，则就是平移了；如果强行w=0，则代表无穷远点；另外如果点每个分量同时乘以一个非零数，大小不变。